来源：小码A梦

二分查找（Binary Search）是一种在有序数组中查找特定元素的高效算法。它的基本思想是将目标值与数组中间的元素进行比较，如果目标值小于中间元素，则在数组的左半部分继续查找，否则在右半部分查找，不断缩小搜索范围，直到找到目标值或确定目标值不存在为止。

二分查找也叫折半查找，比如在一个有序的数组里面找到目标值，它是一种查询效率比较高的算法，时间复杂度O(logn)。比如在下面数组找到 6.首先在定位到两侧，也就是最大值和最小值。并找到中间和目标值比较。

中间值是 23，比目标值更大，就要缩小范围，中间值作为最大值，在中间值左边的区域再找到中间值和目标值比较。

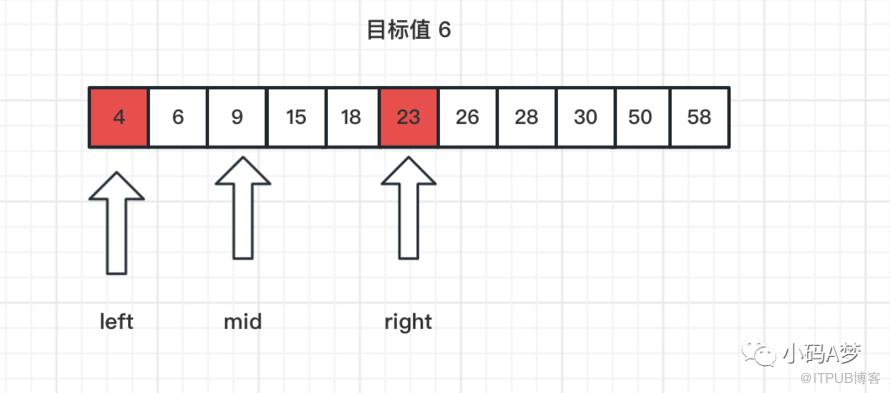
以此类推，一直缩小范围，直到找到目标值，或者搜索完数据。

二分查找模板

public static int binarySearch(int[] nums, int target) {

    int left = 0;

    int right = nums.length - 1;

    while

 (left <= right) {

        int mid = left + (right - left) / 2; // 计算中间元素的索引

        if

 (nums[mid] == target) {

            return

 mid; // 找到目标值，返回索引

        } else if

 (nums[mid] < target) {

            left = mid + 1; // 目标值在右半部分

        } else

 {

            right = mid - 1; // 目标值在左半部分

        }

    }

    return

 -1; // 目标值不存在

}

❝

left 和 right 记录最小值和最大值的下标，left + (right - left) / 2 是查询中间下标，有的查询下标直接使用（left + right）/2，这样可能会超出时间范围。通过 left = mid + 1 或者 right = mid - 1 不断缩小范围。

❞

LeetCode 题解

33.搜索旋转排序数组

题目描述

解题思路

有序的数组在某个下标上进行旋转：

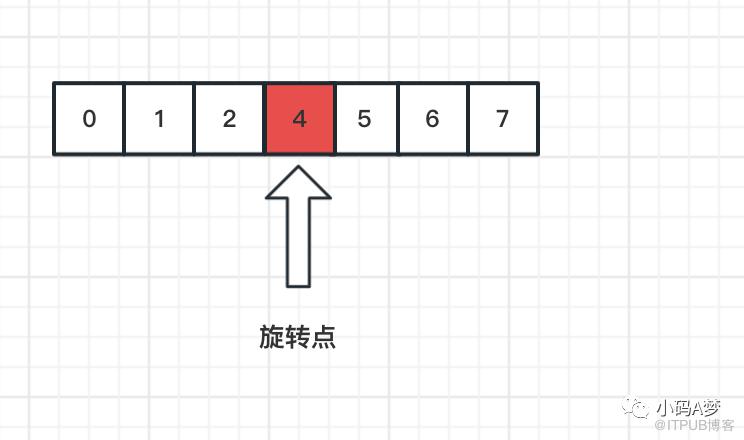
将旋转点之后的数据整体放在数组之前：

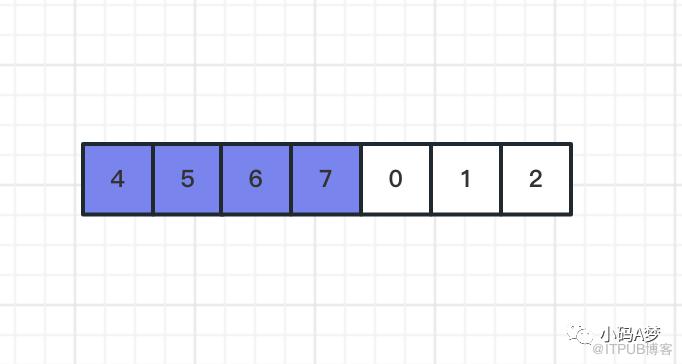
上面说二分查询只是针对有序的数组，这又不是一个有序的数组，但是数组分成两部分有序的数组。

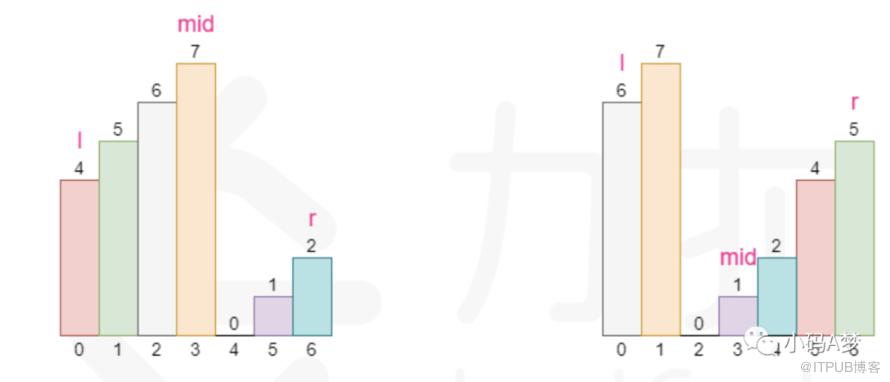
使用二分查找查看由 mid 分割出来的两部分 [l,mid] 和 [mid+1,r] 哪个部分是有序的，并根据有序的那个部分确定二分查找的左右边界如果[l,m-1]是有序数组，并且 target 的大小在 [l,mid] 中，则将搜索目标缩小至[l,mid - 1],否则范围在 [mid + 1，r] 中寻找。如果[mid,r]是有序数组，并且 target 的大小在 [mid + 1,r] 中，则将搜索目标缩小至[mid + 1,r],否则在[l,mid - 1] 中寻找。public int search(int[] nums, int target) {

    int length = nums.length;

    if

 (length == 0) {

        return

 -1;

    }

    if

 (length == 1) {

        return

 nums[0] == target ? 0 : -1;

    }

    int left = 0,right = length-1;

    while

 (left <= right) {

        int mid = left + (right - left)/2;

        if

 (nums[mid] == target) {

            return

 mid;

        }

        if

 (nums[0] <= nums[mid]) {

            if

 (nums[0] <= target && target < nums[mid]) {

                right = mid -1;

            } else

 {

                left = mid + 1;

            }

        } else

 {

            if

 (nums[mid] < target && target <= nums[length - 1]) {

                 left = mid + 1;

            } else

 {

                 right = mid - 1;

            }

        }

    }

    return

 -1;

}

69.x的平方根

题目描述

解题思路

求解平法根，也就是k² <= x，也就是求解 k 最大整数值。对 x 进行二分查找。

左边界是0，右边界是为x，每次二分查找到中间值 mid，mid 的平方的 x 的大小做对比。如果 mid 的平方小于等于 x，赋值结果，并且左边界移动到 mid + 1 的位置。如果 mid 的平方大于x，将有边界移动到 mid - 1 的位置。直达找到最优的解。public int mySqrt(int x) {

    if

 (x == 0 || x == 1) {

        return

 x;

    }

    int left = 1;

    int right = x;

    int result = -1;

    while

 (left <= right) {

        int mid = left + (right - left)/2;

        if

 ((long)mid * mid > x) {

            right = mid - 1;

        } else

 { 

            result = mid;

            left = mid + 1;

        }

    }

    return

 result;

}

153.寻找旋转排序数组中的最小值

题目描述

解题思路

旋转数组是要么全部有序，要么两个部分有序。每次做二分查找，每次mid和最右边值作比较，会出现两种情况。

第一种情况是 nums[pivot] < nums[high]，如上图所示，此时最小值应该在 piot 的左侧，height 缩进到 pivot 的位置。

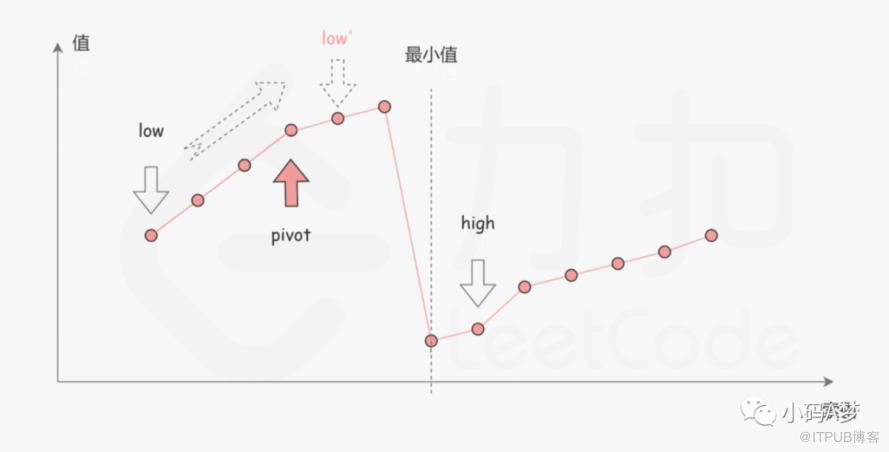
第二种情况是 nums[piot] > num[height], 如上图所示，此时最小值应该在 piot 的右侧，low 缩进到 piot 的位置。

class Solution {

    public int findMin(int[] nums) {

        int low = 0,height = nums.length-1;

     while

 (low < height) {

            int mid = low + (height - low)/2;

            if

 (nums[mid] < nums[height]) {

                height = mid;

            } else

 {

                low = mid + 1;

            }

        }

     return

 nums[low];

    }

}

367.有效的完全平方数

题目描述

解题思路

判断一个数是否是完全平方数，需要找到他的开根数。使用二分法查找，如果 num < 2 返回true，因为 0 和都是完全平方数。2 为 left，num 为 right，通过 left + (right - left)/2 找到中间值如果 mid² = num，返回true。如果 mid² < num,left = mid + 1。如果 mid² > num ,right = mid - 1。public boolean isPerfectSquare(int num) {

    if

 (num <= 2) {

        return true

;

    }

    int left = 2,right = num/2,y;

    long square;

    while

 (left <= right) {

        y = left + (right - left)/2;

        square =(long) y * y;

        if

 (square == num) {

            return true

;

        }else if

 (square > num) {

            right = y - 1;

        }else

 {

            left = y + 1;

        }

    }

    return false

;

}

总结

搜索有序的数组的元素，使用二分查找是一个高效率的查询方法。定位左右两侧最大值和最小值，找到中间值。然后通过目标值和中间值做对比，缩小搜索范围，直到搜索找到符合条件数据。

有时候无需全部有序，两部分有序也是可以通过二分查找找到符合要求的数据。