以后有面试官问你「跳跃表」,你就把这篇文章扔给他

本文字数:4000字
阅读本文大概需要:11 分钟
假如我们要用某种数据结构来维护一组有序的int型数据的集合,并且希望这个数据结构在插入、删除、查找等操作上能够尽可能着快速,那么,你会用什么样的数据结构呢?
数组
一种很简单的方法应该就是采用数组了,在查找方面,用数组存储的话,采用二分法
可以在 O(logn) 的时间里找到指定的元素,不过数组在插入、删除这些操作中比较不友好,找到目标位置所需时间为 O(logn) ,进行插入和删除这个动作所需的时间复杂度为 O(n) ,因为都需要移动移动元素,所以最终所需要的时间复杂度为 O(n) 。
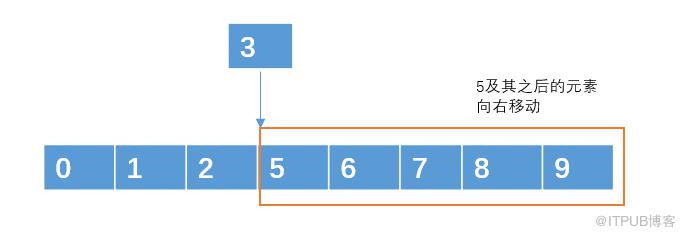
例如对于下面这个数组:
插入元素 3
链表
另外一种简单的方法应该就是用链表了,链表在插入、删除的支持上就相对友好,当我们找到目标位置之后,插入、删除元素所需的时间复杂度为 O(1) ,注意,我说的是找到目标位置之后,插入、删除的时间复杂度才为O(1)。
但链表在查找上就不友好了,不能像数组那样采用二分查找的方式,只能一个一个结点遍历,所以加上查找所需的时间,插入、删除所需的总的时间复杂度为O(n)。
假如我们能够提高链表的查找效率,使链表的查找的时间复杂度尽可能接近 O(logn) ,那链表将会是很棒的选择。
提高链表的查找速度
那链表的查找速度可以提高吗?
对于下面这个链表

假如我们要查找元素9,按道理我们需要从头结点开始遍历,一共遍历8个结点才能找到元素9。能否采取某些策略,让我们遍历5次以内就找到元素9呢?请大家花一分钟时间想一下如何实现?
由于元素的有序的,我们是可以通过增加一些路径来加快查找速度的。例如

通过这种方法,我们只需要遍历5次就可以找到元素9了(红色的线为查找路径)。

还能继续加快查找速度吗?
答是可以的,再增加一层就行了,这样只需要4次就能找到了,这就如同我们搭地铁的时候,去某个站点时,有快线和慢线几种路线,通过快线 + 慢线的搭配,我们可以更快着到达某个站点。

当然,还能在增加一层,

基于这种方法,对于具有 n 个元素的链表,我们可以采取 ** (logn + 1) 层指针路径的形式,就可以实现在 O(logn) 的时间复杂度内,查找到某个目标元素了,这种数据结构,我们也称之为跳跃表,跳跃表也可以算是链表的一种变形,只是它具有二分查找的功能。
插入与删除
上面例子中,9个结点,一共4层,可以说是理想的跳跃表了,不过随着我们对跳跃表进行插入/删除结点的操作,那么跳跃表结点数就会改变,意味着跳跃表的层数也会动态改变。
这里我们面临一个问题,就是新插入的结点应该跨越多少层?
这个问题已经有大牛替我们解决好了,采取的策略是通过抛硬币来决定新插入结点跨越的层数:每次我们要插入一个结点的时候,就来抛硬币,如果抛出来的是正面,则继续抛,直到出现负面为止,统计这个过程中出现正面的次数,这个次数作为结点跨越的层数。
通过这种方法,可以尽可能着接近理想的层数。大家可以想一下为啥会这样呢?
插入
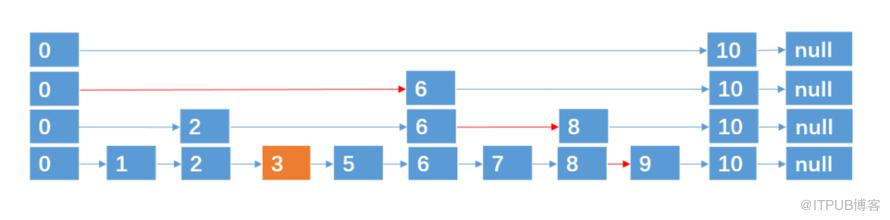
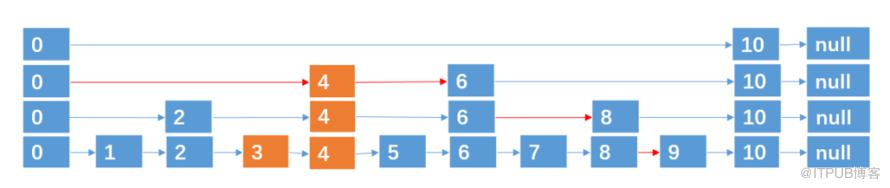
例如,我们要插入结点 3,4,通过抛硬币知道3,4跨越的层数分别为 0,2 (层数从0开始算),则插入的过程如下:
插入 3,跨越0层。
插入 4,跨越2层。
删除
解决了插入之后,我们来看看删除,删除就比较简单了,例如我们要删除4,那我们直接把4及其所跨越的层数删除就行了。

小结
跳跃表的插入与删除至此都讲完了,总结下跳跃表的有关性质:
(1). 跳跃表的每一层都是一条有序的链表.
(2). 跳跃表的查找次数近似于层数,时间复杂度为O(logn),插入、删除也为 O(logn)。
(3). 最底层的链表包含所有元素。
(4). 跳跃表是一种随机化的数据结构(通过抛硬币来决定层数)。
(5). 跳跃表的空间复杂度为 O(n)。
跳跃表 vs 二叉查找树
有人可能会说,也可以采用二叉查找树啊,因为查找查找树的插入、删除、查找也是近似 O(logn) 的时间复杂度。
不过,二叉查找树是有可能出现一种极端的情况的,就是如果插入的数据刚好一直有序,那么所有节点会偏向某一边。例如
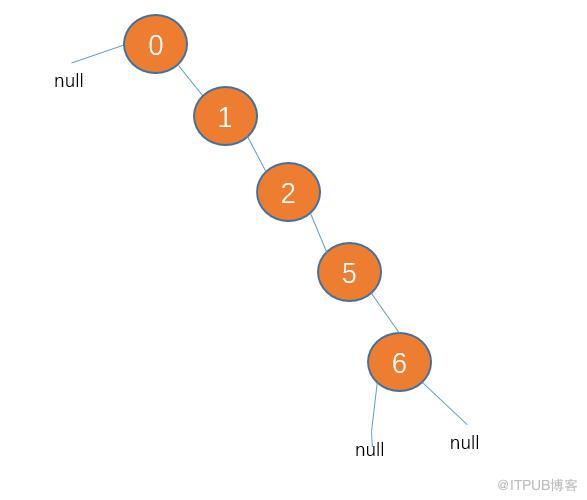
这种接结构会导致二叉查找树的查找效率变为 O(n),这会使二叉查找树大打折扣。
跳跃表 vs 红黑树
红黑可以说是二叉查找树的一种变形,红黑在查找,插入,删除也是近似O(logn)的时间复杂度,但学过红黑树的都知道,红黑树比跳跃表复杂多了,反正我是被红黑树虐过。在选择一种数据结构时,有时候也是需要考虑学习成本的。
而且红黑树插入,删除结点时,是通过调整结构来保持红黑树的平衡,比起跳跃表直接通过一个随机数来决定跨越几层,在时间复杂度的花销上是要高于跳跃表的。
当然,红黑树并不是一定比跳跃表差,在有些场合红黑树会是更好的选择,所以选择一种数据结构,关键还得看场合。
总上所述,维护一组有序的集合,并且希望在查找、插入、删除等操作上尽可能快,那么跳跃表会是不错的选择。redis 中的数据数据便是采用了跳跃表,当然,ridis也结合了哈希表等数据结构,采用的是一种复合数据结构。
代码如下
1//节点 2class Node{
3 int value = -1;
4 int level;//跨越几层 5 Node[] next;//指向下一个节点 6 7 public Node(int value, int level){
8 this.value = value;
9 this.level = level;
10 this.next = newNode[level];
11}
12}
13//跳跃表 14public class SkipList{
15 //允许的最大层数 16 int maxLevel = 16;
17 //头节点,充当辅助。 18 Node head = new Node(-1, 16);
19 //当前跳跃表节点的个数 20 int size = 0;
21 //当前跳跃表的层数,初始化为1层。 22 int levelCount = 1;
23 24 25 public Node find(int value){
26Node temp = head;
27 for (int i = levelCount - 1; i >= 0; i--) {
28 while (temp.next[i] != null && temp.next[i].value < value) {
29temp = temp.next[i];
30}
31}
32 //判断是否有该元素存在 33 if (temp.next[0] != null && temp.next[0].value == value) {
34 System.out.println(value + " 查找成功");
35 return temp.next[0];
36 } else{
37 return null;
38}
39}
40 // 为了方便,跳跃表在插入的时候,插入的节点在当前跳跃表是不存在的 41 //不允许插入重复数值的节点。 42 public void insert(int value){
43 intlevel = getLevel();
44 Node newNode = new Node(value, level);
45 //update用于记录要插入节点的前驱 46 Node[] update = newNode[level];
47 48Node temp = head;
49 for (int i = level - 1; i >= 0; i--) {
50 while (temp.next[i] != null && temp.next[i].value < value) {
51temp = temp.next[i];
52}
53update[i] = temp;
54}
55 //把插入节点的每一层连接起来 56 for (int i = 0; i < level; i++) {
57newNode.next[i] = update[i].next[i];
58update[i].next[i] = newNode;
59}
60 //判断是否需要更新跳跃表的层数 61 if(level > levelCount) {
62levelCount = level;
63}
64size++;
65 System.out.println(value + " 插入成功");
66}
67 68 public void delete(int value){
69 Node[] update = newNode[levelCount];
70Node temp = head;
71 72 for (int i = levelCount - 1; i >= 0; i--) {
73 while (temp.next[i] != null && temp.next[i].value < value) {
74temp = temp.next[i];
75}
76update[i] = temp;
77}
78 79 if (temp.next[0] != null && temp.next[0].value == value) {
80size--;
81 System.out.println(value + " 删除成功");
82 for (int i = levelCount - 1; i >= 0; i--) {
83 if (update[i].next[i] != null && update[i].next[i].value == value) {
84update[i].next[i] = update[i].next[i].next[i];
85}
86}
87}
88}
89 90 //打印所有节点 91 public void printAllNode(){
92Node temp = head;
93 while (temp.next[0] != null) {
94 System.out.println(temp.next[0].value + " ");
95 temp = temp.next[0];
96}
97}
98 99 //模拟抛硬币100 private int getLevel(){
101 int level = 1;
102 while (true) {
103 int t = (int)(Math.random() * 100);
104 if (t % 2 == 0) {
105level++;
106 } else{
107 break;
108}
109}
110 System.out.println("当前的level = "+ level);
111 returnlevel;
112}
113114 //测试数据115 public static void main(String[] args){
116 SkipList list = newSkipList();
117 for (int i = 0; i < 6; i++) {
118list.insert(i);
119}
120list.printAllNode();
121 list.delete(4);
122list.printAllNode();
123 System.out.println(list.find(3));
124 System.out.println(list.size + " "+ list.levelCount);
125}
126}扫一扫,关注我们

